Generator

What Can Generator Do?

Generator is a computer program that can help you solve a wide variety of problems, whether they are complex or simple. It's designed to interact with Microsoft Excel(tm) worksheets. Basically, if you can define your problem in an Excel worksheet, you can use Generator to find a solution. You can use Generator to maximize profits, minimize costs, or solve equations. All you need is an Excel worksheet with input variables and a single output expression which describes the quality of a solution (eg., cost, profit, etc.). You can use Generator to maximize profits, minimize costs, or solve equations. Generator is designed to run on IBM compatible computers under Windows and NT, and is Y2K compliant.

A few examples....... Generator can be used to:

solve complex routing and scheduling problems
design electronic circuits
maximize profit
curve fit
improve factory efficiency
solve coupled sets of nonlinear partial differential equations
optimize dynamic systems

As you can see, all sorts of problems can be solved using Generator! It's POWERFUL!

Generator is the latest genetic algorithm software available designed to interact with Microsoft Excel worksheets. It is also the most advanced. In this brochure, we'll tell you all about Generator and its features, and how it can be used for different applications. Genetic algorithms will first be reviewed, and then we'll outline how Generator harnesses evolutionary principles to arrive at a solution. We will also detail all of the features available in Generator, and how these feature make Generator the most powerful product of its kind on the market. Some applications will also be discussed, including some performance comparisons with our nearest competitor.

System Requirements

Generator requires at least a 386 IBM(tm) compatible computer with 2 MB of RAM, with Microsoft Windows 3.x, Windows 95 or NT, and Excel 4, Excel 5, Excel for Windows 95, or Office 97 {English Versions Only!} . The program will run considerably faster if a later model computer with more memory is used.

Warning: Generator does not work foreign language versions of Excel.

Genetic Algorithms

Applications which use genetic algorithms to solve problems are surfacing in a wide range of areas. Over 500 research articles were published in 1994 alone on genetic algorithms, and widespread interest in these computer programs is increasing. Genetic algorithms are essentially a software version of the evolutionary process. The main difference is the computer process can be greatly accelerated by fine-tuning and manipulating the evolutionary principles, where members of the population are born, mate, and die in a few microseconds. This allows for enormous change to occur rapidly.

Genetic algorithms require a set of population members, usually numbering between 20 to 100. Each population member represents a trial solution to a given problem. The trial solution - where numbers are used for the input variables - is tested by an evaluation function, which calculates the quality of the trial solution. The output is commonly called the Fitness, since it describes how "fit" the trial solution is.

The inputs for the fitness function are often called genes, chromosomes, or genomes. For Generator, we refer to them as "genes". The fitness function typically has a number of different inputs. For instance, if the fitness function for a factory calculates the factory's profit, the input variables, or genes, may consist of worker overtime, supply costs, productivity, QA efforts, process variables, etc. Each population member will therefore have an identical number of genes, or input variables.

Genetic Algorithms work by starting with relatively poor trial solutions, that is, population members with poor fitness. Three basic processes are then allowed to occur: mating, mutation, and selection ("survival of the fittest"). The first process, mating, involves an exchange of information between population members, something which is referred to as crossover. When population members mate, they cross gene values over to their partner, resulting in an exchange of gene values. This rearranges the information in the gene values of the population members, creating new and diverse "offspring" that combine potentially beneficial features of their parents.

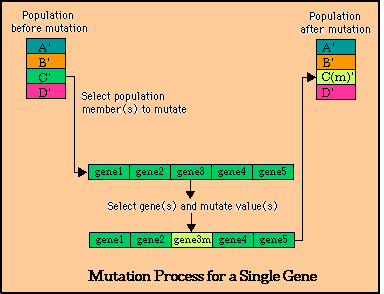
Once the crossover has taken place, the offspring undergo mutation. In mutation, the values of the individual genes of population members can be changed, or mutated. Mutation is important in evolution because unlike crossover (which merely trades genes), new gene values are introduced. This further increases the diversity of the population members.

"Survival of the fittest" principles complete the evolutionary cycle. Once crossover and mutation have occurred, the new population members will replace the old ones if they are better. In this fashion, population members can have improved fitness with each new cycle (or generation) of crossover, mutation, and natural selection. Program users typically want to maximize or minimize the fitness, so the survival of the fittest action is governed by whether the new fitness is better or worse than the previous generation's fitness. The resulting process yields a steadily improving solution to the problem, often identifying the optimum solution in a surprisingly short time.

How Generator Works

Generator employs all of the basic evolutionary processes: crossover, mutation, and natural selection. What distinguishes Generator from other commercial genetic algorithm software is that in Generator, users can fine-tune these parameters on the fly. In addition, Generator has special hill climbing features, recombination operators and mate selection processes to rapidly find the best solution.

Generator will work on problems which involve permutations (re-arranging the order of things), real numbers, and integer numbers. Generator begins working on a problem by creating a random population of trial solutions. A population of up to 100 members can be specified, although the default population of 20 members usually works best. Each trial solution is inserted into the Excel(tm) worksheet, and the quality of the solution, or fitness, is recorded by Generator. This allows the trial solutions to be ordered according to their fitness.

The crossover process in Generator is governed by the fitness of the population members (users may also elect to skip the crossover process). A "roulette wheel" approach is used for mate selection, and each member of the population is allowed to mate and produce an offspring. Population members with the best fitness are given the most slots on the roulette wheel. For instance, if there are four population members ranked according to their fitness (with member "A" being the best), the mate selection roulette wheel would have four slots marked with member "A", three slots marked with member "B", two slots for member "C", and one slot for member "D". Therefore, to find a mate for member "A", we "spin" the wheel until it rests on a member other than "A". The process is repeated so that each population member selects a mate.

Generator then decides how much information is swapped between the different population members. This is done by randomly creating two "cut points" where the genes located in between the two "cuts" are switched. The resulting population member is then referred to as an offspring. This is illustrated below.

Once crossover has taken place, Generator determines a) which population members may undergo mutation, b) which genes of these population members will mutate, and c) how much mutation these genes will undergo. As a user of Generator, you have full control over these parameters, as shown from the Generator screen below:

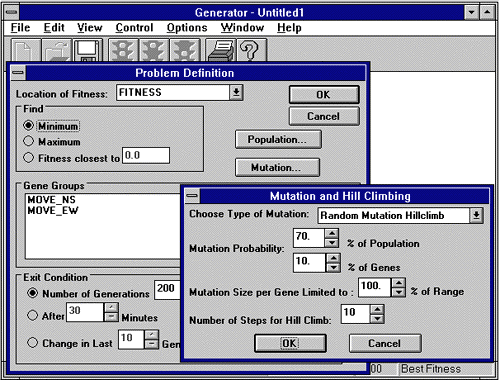
For Random Mutation, Generator randomly selects the population members which undergo mutation according to the Population Mutation Probability. Generator then randomly selects the genes that will be mutated. Population members are selected undergo a second selection to determine which genes will be mutated, according to the Gene Mutation Probability. Next, each gene selected is mutated using a random number and the Percent of the Range. Once the mutation amount has been calculated, it is either added to or subtracted from the original gene. The new value of the gene is checked to make sure that it does not go outside the specified range. The overall mutation process is shown below:

The mutation hill climbing features in Generator provide an opportunity to find solutions fasterin certain kinds of problems. Two types of hill climbing are provided: random mutation hill climbing, and directional hill climbing. In random mutation hill climbing, the user specifies how many random mutations can take place before finishing the random mutation process. For instance, if five steps are specified, up to five mutations will occur consecutively, as long as the mutations result in improvement. Directional hill climbing, on the other hand, examines the results of the first mutation, and allows more identical mutations to occur if the first mutation resulted in improvement. The mutation strategy (random, random mutation hill climb, or directional hill climb) will depend upon the problem. The multiple strategies available in Generator give the user the flexibility needed solve the problem optimally, and strategies are fully detailed in the user's manual!

The generation is complete once the "survival of the fittest" strategy is implemented at the end of the mutation process. Once the mutation process is finished, the population members are re-ordered according to their fitness. This new list is compared to the "old" list (before crossover and mutation). Members from the old list are allowed to replace members of the new list if they are better. In this fashion, if the crossover and mutation result in worse population members, the best solutions are not lost. The user is allowed to specify how many of the old population members can be carried over to the next generation. This flexibility is very important, and control of this parameter allows for much faster solution speed in some instances.

Generator also solves permutation problems. The strategy is similar to real and integer number problems, but the strategy for crossover and mutation is different and proprietary.

Generator can be set to run for a specific length of time, a certain number of generations, or until the solution remains unchanged over time. The history graph in Generator shows the progress of the solution, (see example #4 below) and Excel(tm) can be updated every generation with the values of the best population member.

Performance and Applications

By giving the user a high level of control over the mutation and hill climbing strategies, strategies can be tailored to each problem. Detailed examples in the operator's manual provide insight and advice into specifying these parameters. By tailoring the evolutionary principles to suit each problem, large gains in performance can be obtained. Generator permits the user to control many of the features of the solution process and has advanced hill climbing features which are unavailable in our nearest competitor. As a result, Generator runs significantly faster.

1. Traveling Salesman Problem

This classic problem is often the test of merit for genetic algorithms. Basically, the problem involves trying to find the shortest route between twenty cities by arranging them in the proper order. Our test runs using Generator resulted in an optimal solution for a 20-city problem in about 20 minutes (on a 486 DX computer).

2. Insecticide Placement

We created an example problem for our user's manual where three cans of insecticide must be used to get rid of insects living in a dozen nests. The cans have a fixed "kill" radius, and placing them in different locations will either decrease or increase the number of wasps killed.

3. Curve Fitting

When making silicon computer chips, part of the processing involves coating the silicon wafer with photoresist, and then exposing and developing the photoresist to form patterns for circuit formation. Recently, New Light Industries and other research groups have developed methods to form sub- micron sized 3-dimensional shapes in photoresist by using partial electron- beam exposure. We have used Generator to fit a photoresist depth versus electron-beam exposure curve, shown below (the blue line is the experimental data, the red line is the fit by Generator):

Finding an equation to fit the data gives a better understanding of the process and helps predict depths for different exposures. The notches on the curve are the result of different electron-beam current settings (multiple passes of a high and low current beam). Standard curve fitting routines are useless on this type of data, since the curve is not continuous. Generator, on the other hand, helped us to find the coefficients for an equation which fits the data quite well and at the same time gave us some important insights into the physical mechanisms of the process.

4. Thermoelectric Coolers

Thermoelectric coolers work by passing current through a specially designed diode. The current flowing into the diode carries less heat than the current flowing out, so the diode junction cools. The equations which govern these devices are quite complex (coupled differential equations). The situation becomes much more complex when a cascade configuration is used - that is, the thermoelectric coolers are "stacked" to create a bigger temperature drop than can be achieved for a single diode. The temperature equations for coupled thermoelectric devices consist of a large set of differential equations which depend on the working temperatures of each individual diode. When the temperatures have been correctly solved, the equations will all balance nicely. Solving for these temperatures, however, is a math nightmare.

We used Generator to quickly find the set of temperatures that balance the equations. This saved us the trouble of trying to solve a large set of differential equations the hard way.

5. Optimal Routing

Another example problem in our manual involves finding the best route for a power line through a city. We simulated the city by defining a 10x10 city grid, with different costs at each grid. Twenty moves were then provided on an Excel(tm) worksheet to find the best route from one end of the grid to the other. This problem contains a local optima, which tends to "trap" the solution at the wrong value. Generator is able to locate alternate solutions much better than the competition's software. Generator took an average time of 5.5 hours to find the solution.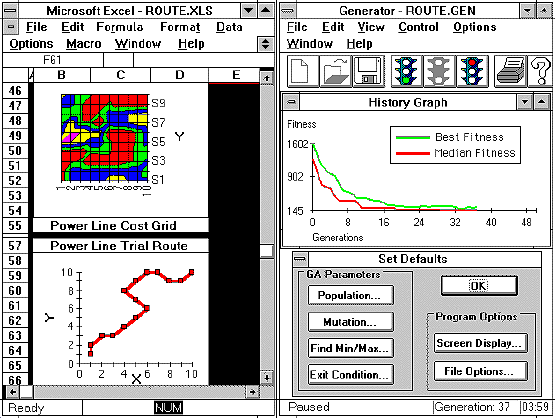

Many other applications of Generator are possible!

A demo version of this program is available on the demos page.